¿Te has preguntado por qué unos ahorran sin esfuerzo y otros no ven cambios significativos?
El interés compuesto es el principio de «interés sobre interés»: los rendimientos se suman al capital y generan nuevos rendimientos en cada periodo. En esta guía verás cómo funciona interés aplicado con distintas tasas y frecuencias.
Te explicaré la fórmula A = P (1 + r/n) ^ nt, la Regla del 72 para estimar duplicaciones, y por qué empezar temprano beneficia el largo plazo. También hablaremos de productos en México como CETES y herramientas de Banxico.
Atención: toda inversión conlleva riesgos y los rendimientos no están garantizados. Usaremos ejemplos en USD, MXN, PEN y COP para que compares escenarios y decidas con más claridad.
Conclusiones clave
- Entenderás el efecto acumulativo del interés sobre el capital.
- Verás cómo la tasa y la frecuencia influyen en resultados.
- Aprenderás a usar la Regla del 72 para estimar plazos.
- Conocerás opciones locales como CETES y simuladores de Banxico.
- Recordarás que no hay garantías: toda inversión implica riesgo.
Qué es el interés compuesto y por qué puede acelerar el crecimiento de tu dinero
Cuando sumas intereses al capital de forma constante, el balance comienza a aumentar sobre sí mismo. En cada periodo la tasa se aplica a un saldo mayor, por lo que los rendimientos no son siempre iguales.
Esto es distinto al interés simple, donde la tasa solo opera sobre el monto inicial. Con capitalización anual, mensual o diaria, la frecuencia determina el impacto acumulado.
El efecto se nota más con el paso de los años: mientras más tiempo dejas la inversión, más aporta la reinversión de rendimientos. Sin embargo, no hay garantías.
Importante: toda inversión está sujeta a riesgos de mercado, costos y variaciones en las tasas. Por eso debes evaluar productos y plazos antes de decidir.
- Sumas los intereses al capital y el nuevo saldo genera más rendimiento.
- Frecuencia y tasa afectan cuánto se acelera el crecimiento.
- Aplica a cuentas, fondos y bonos con reinversión; revisa costos e impuestos.
Si quieres profundizar en cómo funciona etapa por etapa, revisa este artículo sobre interés compuesto y creación de riqueza.
Interés compuesto vs. interés simple: diferencias clave que debes entender
La clave está en si los rendimientos se reinvierten o se calculan siempre sobre el capital inicial. Esta distinción define cuánto cambia tu saldo cada año y qué tan rápido aumentan los pagos o cobros.
Definición práctica: “interés sobre interés” frente a interés solo sobre capital
Con interés simple la tasa se aplica siempre al capital inicial. El interés por periodo es constante.
Con interés compuesto, los rendimientos se suman al saldo y la tasa opera sobre un monto mayor en cada periodo.
Cómo cambia el capital cada año: efecto multiplicador
A 5% anual sobre $10,000, el método simple genera $1,500 en 3 años.
El método con reinversión genera aproximadamente $1,576.25 en el mismo periodo. La diferencia aumenta con el tiempo.
Cuándo conviene cada uno en ahorro, inversiones y créditos
Para ahorro e inversiones, el sistema con reinversión suele ser preferible por su potencial acumulado, aunque no garantiza rendimientos.
En créditos, la capitalización frecuente puede elevar el costo total si no amortizas. Sistemas de cuotas fijas, como el francés, reducen saldo de forma programada.
- Interés simple: claridad y cálculos rápidos.
- Interés con reinversión: mejor para horizontes largos.
- Créditos: revisa frecuencia de capitalización y amortizaciones.
| Concepto | Interés simple | Interés con reinversión |
|---|---|---|
| Cálculo | Tasa sobre capital inicial | Tasa sobre capital + intereses |
| Interés por año | Constante | Creciente |
| Ideal para | Instrumentos cortos o cálculo rápido | Ahorro e inversiones a mediano-largo plazo |
Cómo calcular interés compuesto paso a paso
Aprender a calcular el saldo final paso a paso te dará control sobre tus decisiones financieras. Aquí verás la fórmula y cómo interpretar cada variable para estimar un monto proyectado.
Desglose de la fórmula principal
A = P (1 + r/n) ^ nt
P es el capital inicial. r es la tasa interés anual en decimal. n es el número de periodos por año. t es el tiempo en años.
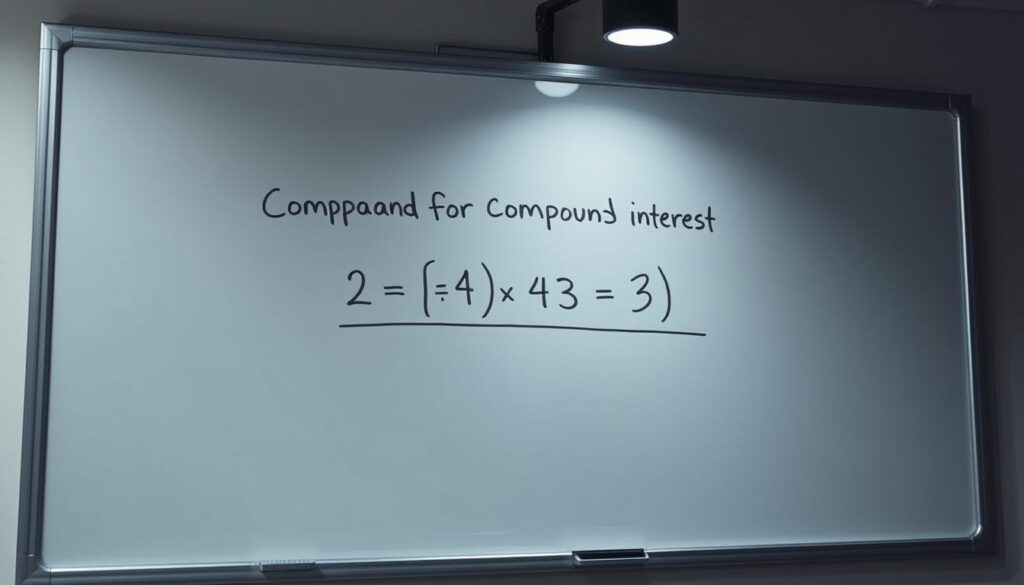
Alternativa para calcular sólo intereses
Si solo quieres conocer los intereses acumulados, usa P[(1+i)^n – 1], donde i es la tasa por periodo y n el número total de periodos.
- Con $10,000 a 5% anual por 3 años y capitalización anual, los intereses aproximados son $1,576.25.
- A mayor número de periodos por año (por ejemplo mensual o diaria), mayor será el saldo final.
- En México, cuentas de ahorro suelen capitalizar diario; depósitos a plazo, mensualmente; tarjetas, diario (esto eleva el costo si tienes deuda).
Dominar la fórmula te ayuda a comparar opciones, pero valida resultados con calculadoras fiables y considera impuestos y comisiones. Para una guía práctica sobre conceptos básicos visita esta guía. Recuerda que invertir conlleva riesgos y no hay rendimientos garantizados.
interes compuesto ejemplo que puedes replicar hoy
Empieza con un plan claro y configura la reinversión automática para que no tengas que intervenir. Esto te permite comprobar en la práctica cómo funciona el interés compuesto.
Pasos concretos: define objetivo, tasa estimada, plazo y automatiza la reinversión
Primero, define tu objetivo: fondo de emergencia, retiro o una meta intermedia. El plazo determina cuánto puede aportar la acumulación en el largo plazo.
Segundo, estima una tasa realista según el instrumento y el riesgo. No hay rendimientos garantizados; los valores pueden variar.
Tercero, automatiza la reinversión (por ejemplo en cetesdirecto o con DRIP de dividendos) para que los intereses se sumen al capital sin intervención.
Para que lo pruebes ahora: invierte €/$10,000 a 3% anual. A 4 años tendrás ≈ 11,255; a 12 años ≈ 14,260; y a 24 años ≈ 20,192. Estos números muestran el efecto del tiempo.
- Agrega aportes periódicos si puedes; aceleran resultados y reducen volatilidad.
- Revisa costos, impuestos y liquidez antes de ejecutar la inversión.
- Monitorea avances cada trimestre; evita revisar diariamente para preservar el enfoque en el largo plazo.
Recuerda: toda inversión implica riesgos. Usa este ejemplo como una guía práctica y ajusta cifras según tus condiciones en México y LATAM.
Dónde aplicarlo en Latinoamérica: México, Perú y Colombia
Si vives en México, Perú o Colombia, hay alternativas concretas para que tus aportes trabajen con el tiempo. Conocer las opciones locales te ayuda a elegir productos que permitan reinversión automática y mejor capitalización.
México
En México puedes empezar en CETES vía cetesdirecto desde montos bajos y activar reinversión automática. Tus aportes a la Afore también se benefician con el tiempo, aunque los rendimientos fluctúan.
Apps y fondos como GBM ofrecen planes que reinvierten dividendos para impulsar tus inversiones y tu ahorro; revisa comisiones y desempeño histórico.
Perú
En Perú, los depósitos a plazo y fondos mutuos permiten capitalización periódica. Los bonos en soles o dólares pagan cupones que, si reinviertes, aumentan el efecto del interés compuesto.
Verifica la tasa y el plazo; los rendimientos no están garantizados y conviene comparar alternativas antes de decidir.
Colombia
En Colombia, los CDT y los fondos de inversión colectiva (FIC) ofrecen opciones según plazo y perfil. Los TES pueden pagarte cupones que se reinvierten si así lo programas.
Evalúa la tasa interés efectiva, impuestos y costos para estimar el rendimiento real.
- Consejo: compara la capitalización y la tasa efectiva anual en cada producto.
- Riesgo: toda inversión implica incertidumbre; no hay garantías.
Ejemplos con números reales en USD y moneda local
A continuación te presento cálculos claros para comparar resultados según la frecuencia de capitalización y la tasa aplicada.
USD: con $10,000 a 5% por 10 años, el interés simple suma $5,000 y el saldo final sería $15,000.
Si aplicas capitalización anual, el monto estimado es ≈ $16,289. Con capitalización mensual sube a ≈ $16,470. Esto ilustra el valor del interés compuesto y por qué conviene saber calcular interés según la frecuencia.
«No hay garantías: las tasas cambian y toda inversión implica riesgo.»
Regla del 72 como guía rápida
Usando la Regla del 72, a 4% duplicas en ~18 años; a 6% en ~12 años. Es una aproximación útil para estimar cuántos años necesitará un monto para duplicarse según la tasa interés.

MXN, PEN y COP: comparación a 5 años (5% anual)
| Moneda | Inicial | Capitalización anual (≈) | Capitalización mensual (≈) |
|---|---|---|---|
| MXN | $10,000 | $12,762 | $12,834 |
| PEN | S/ 1,000 | S/ 1,276 | S/ 1,283 |
| COP | $1,000,000 | $1,276,280 | $1,283,360 |
Estos números muestran que la diferencia entre anual y mensual es pequeña a corto plazo, pero se amplía con los años. Usa una calculadora para validar cifras según la tasa y el horizonte que consideres.
- Este ejemplo te ayuda a comparar montos y entender la influencia de la capitalización.
- Recuerda que el resultado final depende de la tasa y del tiempo; pequeñas variaciones afectan mucho en horizontes largos.
Aportes periódicos: la forma más simple de hacer crecer dinero con constancia
Pequeñas aportaciones regulares pueden transformar tus metas financieras con menos esfuerzo del que imaginas.
La clave es combinar constancia y automatización. Programa débitos mensuales para que tus aportes se reinviertan sin que tengas que decidir cada mes.
Simulación con aportes mensuales y reinversión automática en el largo plazo
Con un capital inicial de $10,000 y aportes de $100/mes a 3% anual por 25 años, el saldo supera los $65,000. Esto muestra cómo el tiempo favorece tu plan.
Si aportas $500/mes a 7% anual durante 10 años, el resultado supera los $85,000; aproximadamente $25,000 provienen de los rendimientos acumulados.
Considera riesgos: las tasas varían, hay comisiones e impuestos. Revisa liquidez y elige instrumentos que permitan reinversión automática.
- Automatiza aportes para mantener el hábito.
- Fija una tasa conservadora y revisa supuestos anualment e.
- Prioriza constancia: comenzar temprano multiplica el efecto con el tiempo.
| Escenario | Capital inicial | Aporte mensual | Tasa (anual) | Plazo | Saldo aproximado |
|---|---|---|---|---|---|
| Ahorro largo | $10,000 | $100 | 3% | 25 años | $65,000+ |
| Ahorro agresivo | $0 | $500 | 7% | 10 años | $85,000+ |
| Comienzo temprano | $5,000 | $200 | 4% | 20 años | $80,000≈ |
Cuando el interés compuesto juega en tu contra: tarjetas y préstamos
Las deudas pueden crecer rápido si no revisas cómo se calculan los cargos. En México y LATAM, las tarjetas de crédito suelen aplicar capitalización diaria. Si pagas sólo el mínimo, el saldo aumenta porque los cargos se suman al principal cada periodo.
Crédito y tarjetas con capitalización frecuente
La capitalización diaria encarece el interés efectivo. Una tasa que parece baja puede resultar cara cuando prolongas el plazo o sólo cubres pagos mínimos.
Préstamos con cuotas fijas vs. capitalización
En un préstamo de $1,000 al 3% anual por 2 años con esquema de capitalización compuesta, los intereses totales son ≈ $60.90. Con amortización francesa, la cuota fija mensual sería $42.98 y el costo final ≈ $1,031.55.
- La diferencia está en cómo y cuándo se suman los cargos.
- Paga más que el mínimo para reducir el capital y frenar el efecto acumulado.
- Evalúa el costo total: tasa, frecuencia de capitalización, comisiones y seguros.
Conclusión: prioriza deudas con mayor capitalización y revisa simuladores antes de firmar cualquier contrato de préstamos o crédito.
Herramientas para calcular y decidir con objetividad
Para decidir con datos, necesitas herramientas que conviertan supuestos en resultados claros.
Empieza con calculadoras en línea: la de Investor.gov permite proyectar aportes mensuales y distintos horizontes. En México, Banxico y cetesdirecto ofrecen simuladores para comparar tasas, plazos y reinversión.
Cómo usar hojas de cálculo
En Excel o Google Sheets aplica la fórmula A = P(1+i)^n para obtener el monto final. También puedes hacer un cálculo iterativo año a año o crear una macro simple para automatizar escenarios.
Tres maneras prácticas en hojas de cálculo:
- Cálculo paso a paso (iterativo) para ver cada periodo.
- Fórmula directa A = P(1+i)^n para resultados rápidos.
- Macro personalizada para correr múltiples hipótesis a la vez.
«Toda herramienta entrega estimaciones; documenta supuestos y revisa resultados periódicamente.»
| Recurso | Uso principal | Ventaja |
|---|---|---|
| Investor.gov | Proyecciones con aportes mensuales | Interfaz sencilla y educativa |
| Banxico / cetesdirecto | Simuladores locales | Datos y tasas aplicables en México |
| TheCalculatorSite / Council for Economic Education | Gráficos y comparación principal vs intereses | Visualizaciones educativas |
Consejo: documenta la tasa interés, frecuencia de capitalización y aportes al crear tu escenario. Así valorarás mejor el rendimiento estimado y evitarás sorpresas.
Da tu próximo paso informado: empieza pequeño, sé constante y recuerda que invertir implica riesgos
Toma una decisión informada hoy y deja que el tiempo trabaje a tu favor. Define un objetivo claro, selecciona instrumentos adecuados en México o LATAM y automatiza aportes y reinversión para aprovechar el interés compuesto sin intervenir cada mes.
Mantén expectativas realistas: las tasas pueden variar, los rendimientos no están garantizados y existen impuestos y comisiones que afectan el resultado final. Invierte solo lo que puedas sostener según tu perfil y horizonte de inversión largo.
Usa herramientas confiables (Investor.gov, Banxico, cetesdirecto, Excel) para medir avances. Prioriza pagar deudas con alta capitalización antes de aumentar riesgo en inversiones. Revisa tu plan al menos una vez al año y ajusta aportes, diversificación y tolerancia al riesgo.


